13. Example Cost Function - Lane Change Penalty

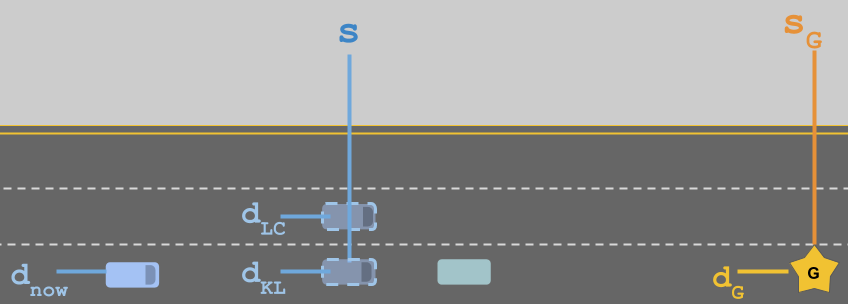
In the image above, the blue self driving car (bottom left) is trying to get to the goal (gold star). It's currently in the correct lane but the green car is going very slowly, so it considers whether it should perform a lane change (LC) or just keep lane (KL). These options are shown as lighter blue vehicles with a dashed outline.

If we want to design a cost function that deals with lane choice, it will be helpful to establish what the relevant variables are. In this case, we can define:

  • \Delta s = s_G - s how much distance the vehicle will have before it has to get into the goal lane.
  • \Delta d = d_G - d_{LC/KL} the lateral distance between the goal lane and the options being considered. In this case \Delta d_{KL} = d_G - d_{KL} would be zero and \Delta d_{LC} = d_G - d_{LC} would not.

Before we define an actual cost function, let's think of some of the properties we want it to have…

First, thinking only about delta d: Would we prefer the absolute value of \Delta d to be big or small ?

SOLUTION: Small

Now let's think about how s factors into our considerations of lane cost. Should costs associated with lane change be more important when we are far from the goal (in s coordinate) or close to the goal?

SOLUTION: Close

So we want a cost function that penalizes large |\Delta d| and we want that penalty to be bigger when \Delta s is small.

Furthermore, we want to make sure that the maximum cost of this cost function never exceeds one and that the minimum never goes below zero.

Which of the following proposals meets these criteria?

Option 1 : \text{cost} = |\Delta d| + \frac{1}{\Delta s}

Option 2 : \text{cost} = \frac{|\Delta d|}{\Delta s}

Option 3 : \text{cost} = 1 - e^{- \frac{|\Delta d|}{\Delta s}}

Which of the options shown above meet the criteria we want (assume \Delta s is always positive)?

SOLUTION: Option 3

In this example, we found that the ratio \LARGE \frac{|\Delta d|}{\Delta s} was important. If we call that ratio x we can then
use that ratio in any function with bounded range. These functions tend to be useful when designing cost functions. These types of functions are called Sigmoid Functions. You can learn more in the Wikipedia article if you're interested.

Next Concept